Euclid
Euclid is a Swift library for creating and manipulating 3D geometry using techniques such as extruding or "lathing" 2D paths to create solid 3D shapes, and CSG (Constructive Solid Geometry) to combine or subtract those shapes from one another.
Euclid is the underlying implementation for the ShapeScript App. Anything you can build in ShapeScript can be replicated programmatically in Swift using this library.
If you would like to support the development of Euclid, please consider buying a copy of ShapeScript (the app itself is free, but there is an in-app purchase to unlock some features).
Note: Euclid is a fairly complex piece of code, at a fairly early stage of development. You should expect some bugs and breaking changes over the first few releases, and the documentation is a little sparse. Please report any issues you encounter, and I will do my best to fix them.
Installation
Euclid is packaged as a dynamic framework that you can import into your Xcode project. You can install this manually, or by using CocoaPods, Carthage, or Swift Package Manager.
Note: Euclid requires Xcode 10+ to build, and runs on iOS 10+ or macOS 10.12+.
To install Euclid using CocoaPods, add the following to your Podfile:
pod 'Euclid', '~> 0.1'
To install using Carthage, add this to your Cartfile:
github "nicklockwood/Euclid" ~> 0.1
To install using Swift Package Manage, add this to the dependencies: section in your Package.swift file:
.package(url: "https://github.com/nicklockwood/Euclid.git", .upToNextMinor(from: "0.1.0")),
Types
The key types defined in the Euclid library are described below:
Vector
The Vector type represents a position or distance in 3D space.
There is no 2D vector type in Euclid, but when working with primarily 2D shapes (such as Paths) you can omit the Z coordinate when constructing a Vector and it will default to zero.
Vertex
The Vertex type is used to construct Polygons to form a Mesh. Each Vertex has the following Vector properties:
position- theVertex's location in 3D spacenormal- the surface normal of aMeshat the vertex's position (used for lighting)texcoord- a 2D texture coordinate used for texture mapping thePolygon
Note: The position of each Vertex is automatically quantized (rounded to the nearest point in a very fine grid) in order to avoid the creation of very tiny polygons, or hairline cracks in surfaces. For that reason, to avoid accumulating rounding errors you should generally avoid applying multiple Transforms to the same geometry in sequence.
Polygon
The Polygon type represents an arbitrary polygon in 3D space. Polygons must have three or more Vertexes, and those vertices must all lie on the same plane. The edge of the Polygon can be either convex or concave, but not self-intersecting.
The Polygon constructor does some basic checks to try to prevent invalid Polygons from being constructed accidentally, but if you are sufficiently determined, you can probably still create something that will display incorrectly (or crash).
Mesh
The Mesh type represents a collection of Polygons that form a solid shape. A Mesh surface can be convex or concave, and can have zero volume (e.g. a flat shape like a square) but should not contain holes or exposed backfaces, otherwise the result of CSG operations on the Mesh will be undefined.
Bounds
The Bounds type represents an axis-aligned bounding box for a 3D shape or collection of shapes, such as Polygons or Meshes.
Plane
The Plane type represents an infinite plane in 3D space. It is defined by a surface normal Vector and a w value that indicates the distance of the center of the Plane from the world origin.
PathPoint
A PathPoint is a control point along a path. PathPoints have a position Vector, but no normal. Instead, the isCurved property is used to indicate if a point is sharp or smooth, allowing the normal to be inferred automatically when required.
Path
A Path is a sequence of PathPoints representing a line or curve formed from straight segments joined end-to-end. A Path can be either open (a polyline) or closed (a polygon), but should not be self-intersecting or otherwise degenerate.
A closed, flat Path can be converted into a Polygon, but it can also be used for other purposes, such as defining a cross-section or profile of a 3D shape.
Paths are typically 2-dimensional, but because PathPoint positions have a Z coordinate, they are not required to be. Even a flat Path (where all points lie on the same plane) can be translated or rotated so that its points do not necessarily lie on the XY plane.
Rotation
A Rotation represents an orientation or rotation in 3D space. Internally, Rotation is stored as a 3x3 matrix, but that's an implementation detail that may change in future. Rotations can be converted to and from an axis vector and angle, or a set of 3 Euler angles (pitch, yaw and roll).
Transform
A Transform combines a Rotation with a pair of Vectors defining the position and scale.
Transforms are a convenient way to store and manipulate the location, orientation and size of Meshes without directly modifying the vertex positions (which can be problematic due to the buildup of rounding errors, as mentioned earlier).
Geometry
You can create a Mesh in Euclid by manually creating an array of Polygons, but that's pretty tedious. Euclid offers a number of helper methods to quickly create complex geometry:
Primitives
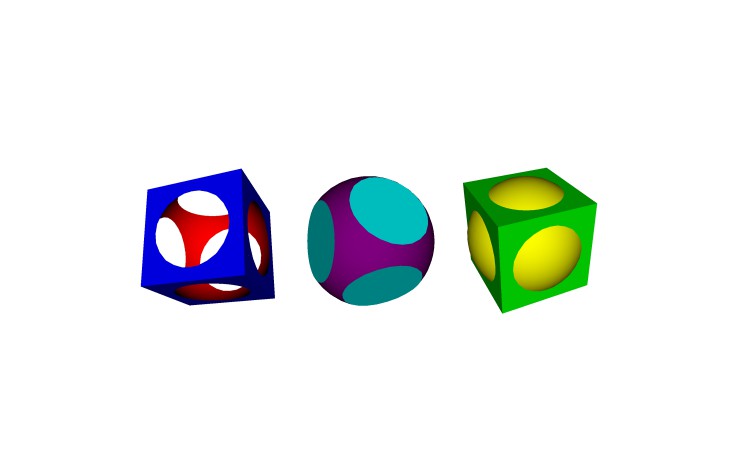
The simplest way to create a Mesh is to start with an existing primitive, such as a cube or sphere. The following primitive types are available in Euclid, and are defined as static constructor methods on the Mesh type:
cube- A cubicMesh(or cuboid, if you specify different values for the width, height and/or depth).sphere- A sphericalMesh.cylinder- A cylindricalMesh.cone- A conicalMesh.
All Meshes are made of flat polygons, and since true curves cannot be represented using straight edges, the sphere, cylinder and cone primitives are actually just approximations. You can control the quality of these approximations by using the slices and/or stacks arguments to configure the level of detail used.
In addition to the 3D Mesh primitives listed, there are also 2D Path primitives. These are implemented as static constructor methods on the Path type instead of Mesh:
circle- A closed, circularPath.rectangle- A closed, rectangularPath.square- Same asrectangle, but with equal width and height.
Builders
Geometric primitives are all very well, but there is a limit to what you can create by combining spheres, cubes, etc. As an intermediate step between the extremes of using predefined primitives or individually positioning polygons, you can use builders.
Builders create a 3D Mesh from a (typically) 2D Path. The following builders are defined as static constructor functions on the Mesh type:
fill- This builder fills a singlePathto create a pair ofPolygons (front and back faces).lathe- This builder takes a 2DPathand rotates it around the Y-axis to create a rotationally symmetricalMesh. This is an easy way to create complex shapes like candlesticks, chess pieces, rocket ships, etc.extrude- This builder fills aPathand extrudes it along its axis. This turns a circular path into a cylinder, or a square into a cube etc.loft- This builder is similar toextrude, but takes multiplePaths and joins them. ThePaths do not need to be the same shape, but must all have the same number of points. To work correctly, thePaths must be pre-positioned in 3D space so they do not all lie on the same plane.
Curves
Builders are a powerful tool for creating interesting Meshes from Paths, but what about creating interesting Paths in the first place?
Creating polygonal Paths by specifying points individually is straightforward, but creating curves that way is tedious. That's where Beziers come in. Beziers allow you to specify complex curves using just a few control points. Euclid exposes this feature via the curve constructor method.
The curve method takes an array of PathPoints and a detail argument. Normally, the isCurved property of a PathPoint is used to calculate surface normals (for lighting purposes), but with the curve method it actually affects the shape of the Path.
Regular (non-curved) PathPoints create sharp corners in the Path as normal, but curved ones are treated as off-curve Bezier control points. The detail argument of the curve method controls how many straight line segments are used to approximate the curve.
The curve method uses second-order (quadratic) Bezier curves, where each curve has two on-curve end points and a single off-curve control point. If two curved PathPoints are used in sequence then an on-curve point is interpolated between them. It is therefore possible to create curves entirely out of curved (off-curve) control points.
This approach to curve generation is based on the popular TrueType (TTF) font system, and provides a good balance between simplicity and flexibility.
CSG
CSG (Constructive Solid Geometry) is another powerful tool for creating intricate geometry. CSG allows you to perform boolean operations (logical AND, OR, etc) on solid shapes. The following CSG operations are defined as methods on the Mesh type:
subtract- Subtracts the volume of oneMeshfrom another.union- Combines two intersectingMeshes, removing internal faces and leaving only the outer shell around both shapes (logical OR).intersection- Returns a singleMeshrepresenting the common volume of two intersectingMeshes (logical AND).stencil- This effectively "paints" part of oneMeshwith the material from another.
All CSG operations require Meshes that are "watertight", i.e. that have no holes in their surface. Using them on Meshes that are not sealed may result in unexpected results.
Rendering
It's all very well creating interesting 3D geometry, but you probably want to actually do something with it.
Most of the Euclid library is completely self-contained, with no dependencies on any particular rendering technology or framework. However, when running on iOS or macOS you can take advantage of Euclid's built-in SceneKit integration. This is demonstrated in the Example app included with the project.
SceneKit is Apple's high-level 3D engine, which can use either OpenGL or Metal for rendering on supported devices. Euclid provides extensions for creating an SCNGeometry from a Mesh, as well as converting Euclid Vector and Rotation types to SCNVector and SCNQuaternion respectively.
The SceneKit integration makes it easy to display Euclid geometry on-screen, and to integrate with ARKit, etc. You can also use SceneKit to export Euclid-generated Meshes in standard 3D model formats such as DAE or OBJ.
Materials
Interesting geometry is all well and good, but to really bring a shape to life it needs colors and textures.
Every Polygon has a material property that can be used to apply any kind of material you like on a per-polygon basis.
All primitives and builder methods accept a material parameter which will apply that material to every polygon in the resultant Mesh. When you later combine meshes using CSG operations, the original materials from the Meshes that contributed to each part of the resultant shape will be preserved.
Since Euclid knows nothing about the material type, it can't do anything with it except pass it around. To use it with SceneKit you need to convert the Euclid material to an SCNMaterial. This can be done using the optional closure argument for the Euclid's SCNGeometry constructor, which receives the Euclid material as an input and returns an SCNMaterial.
Color
Euclid currently has no built-in concept of color, and no support for setting colors on a per-vertex basis, but you can apply colors to a Mesh or Polygon using the material property.
The material property is of type AnyHashable which basically means it can be anything you want. Any NSObject-derived class conforms to AnyHashable, so a simple option is to set the material to be a UIColor or NSColor.
This approach is demonstrated in the Example app included in the project.
Textures
Euclid automatically adds 2D texture coordinates to the vertices of Meshes created using primitives or builder methods. There is limited control over how those coordinates are specified at the moment, but they allow for simple spherical and cylindrical texture wrapping.
To apply a texture image to a Mesh, just store a UIImage or NSImage as the material property and then convert it to an SCNMaterial using the same approach used for colors in the Example app.
If you want to do something more complex, such as applying both a color and texture to the same Mesh, or maybe including a normal map or some other material properties, you could create a custom material type to store all the properties you care about, or even assign an SCNMaterial directly as the material for your Euclid geometry.