SwiftQuantumComputing
Quantum circuit simulator in Swift.
Usage
Build & use a quantum circuit
import SwiftQuantumComputing // for macOS
//: 1. Compose a list of quantum gates. Insert them in the same order
//: you want them to appear in the quantum circuit
let matrix = Matrix([[.one, .zero, .zero, .zero],
[.zero, .one, .zero, .zero],
[.zero, .zero, .zero, .one],
[.zero, .zero, .one, .zero]])
let gates: [Gate] = [
.not(target: 0),
.hadamard(target: 1),
.phaseShift(radians: 0.25, target: 2),
.rotation(axis: .z, radians: 1, target: 3),
.matrix(matrix: matrix, inputs: [3, 2]),
.matrix(matrix: matrix, inputs: [0, 3]),
.oracle(truthTable: ["01", "10"],
controls: [0, 1],
gate: .rotation(axis: .x, radians: 0.5, target: 3)),
.oracle(truthTable: ["0"], controls: [0], target: 2),
.controlled(gate: .hadamard(target: 4), controls: [2]),
.controlled(gate: .matrix(matrix: matrix, inputs: [4, 2]), controls: [1, 0]),
.controlledNot(target: 0, control: 3)
]
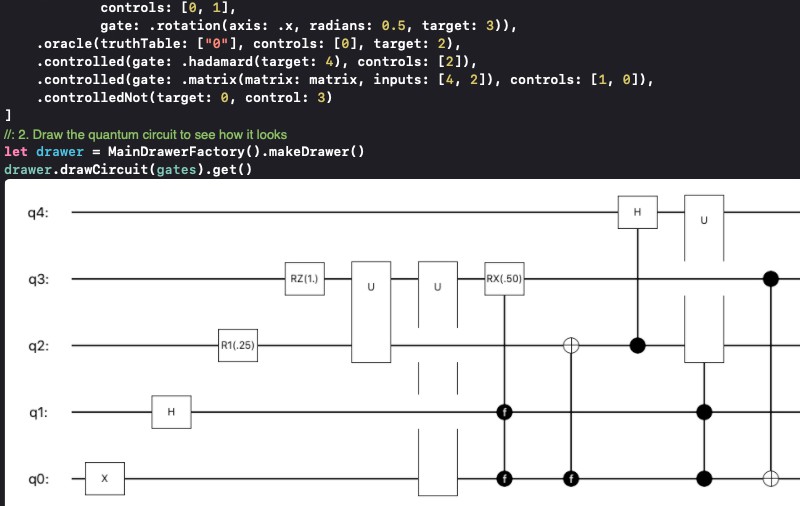
//: 2. (Optional) Draw the quantum circuit to see how it looks
let drawer = MainDrawerFactory().makeDrawer()
drawer.drawCircuit(gates).get()
//: 3. Build the quantum circuit with the list of gates
let circuit = MainCircuitFactory().makeCircuit(gates: gates)
//: 4. Use the quantum circuit
let statevector = circuit.statevector().get()
print("Statevector: \(statevector)\n")
print("Probabilities: \(statevector.probabilities())\n")
print("Summarized probabilities: \(statevector.summarizedProbabilities())\n")
let groupedProbs = statevector.groupedProbabilities(byQubits: [1, 0],
summarizedByQubits: [4, 3, 2]).get()
print("Grouped probabilities: \(groupedProbs)")
print("Unitary: \(circuit.unitary().get())\n")
Check full code in Circuit.playground.
Draw a quantum circuit
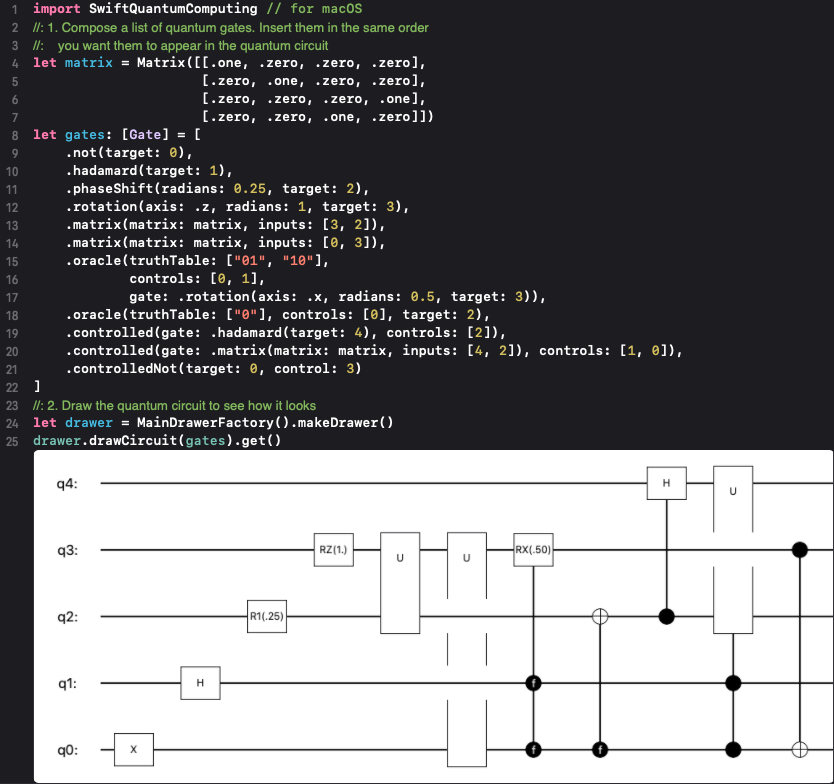
Check full code in Drawer.playground.
Algorithms
Use a genetic algorithm to automatically generate a quantum circuit
import SwiftQuantumComputing // for macOS
//: 0. Auxiliar functions
func configureEvolvedGates(in evolvedCircuit: GeneticFactory.EvolvedCircuit,
with useCase: GeneticUseCase) -> [Gate] {
var evolvedGates = evolvedCircuit.gates
if let oracleAt = evolvedCircuit.oracleAt {
if case .oracle(_, let controls, let gate) = evolvedGates[oracleAt].simplified,
case .not(let target) = gate {
evolvedGates[oracleAt] = Gate.oracle(truthTable: useCase.truthTable.truth,
controls: controls,
target: target)
} else {
fatalError("No oracle found")
}
}
return evolvedGates
}
func drawCircuit(with evolvedGates: [Gate], useCase: GeneticUseCase) -> SQCView {
let drawer = MainDrawerFactory().makeDrawer()
return try! drawer.drawCircuit(evolvedGates, qubitCount: useCase.circuit.qubitCount).get()
}
func probabilities(in evolvedGates: [Gate], useCase: GeneticUseCase) -> [String: Double] {
let circuit = MainCircuitFactory().makeCircuit(gates: evolvedGates)
let initialStatevector = try! MainCircuitStatevectorFactory().makeStatevector(bits: useCase.circuit.input).get()
let finalStatevector = try! circuit.statevector(withInitialStatevector: initialStatevector).get()
return finalStatevector.summarizedProbabilities()
}
//: 1. Define a configuration for the genetic algorithm
let config = GeneticConfiguration(depth: (1..<50),
generationCount: 2000,
populationSize: (2500..<6500),
tournamentSize: 7,
mutationProbability: 0.2,
threshold: 0.48,
errorProbability: 0.000000000000001)
//: 2. Also the uses cases, i.e. the circuit outputs you want to get
//: when the oracle is configured with the different truth tables
let cases = [
GeneticUseCase(emptyTruthTableQubitCount: 1, circuitOutput: "00"),
GeneticUseCase(truthTable: ["0", "1"], circuitOutput: "00"),
GeneticUseCase(truthTable: ["0"], circuitOutput: "10"),
GeneticUseCase(truthTable: ["1"], circuitOutput: "10")
]
//: 3. And which gates can be used to find a solution
let gates: [ConfigurableGate] = [HadamardGate(), NotGate()]
//: 4. Now, run the genetic algorithm to find/evolve a circuit that solves
//: the problem modeled with the use cases
let evolvedCircuit = MainGeneticFactory().evolveCircuit(configuration: config,
useCases: cases,
gates: gates).get()
print("Solution found. Fitness score: \(evolvedCircuit.eval)")
for useCase in cases {
//: 5. (Optional) Draw the solution
let evolvedGates = configureEvolvedGates(in: evolvedCircuit, with: useCase)
drawCircuit(with: evolvedGates, useCase: useCase)
//: 6. (Optional) Check how well the solution found meets each use case
let probs = probabilities(in: evolvedGates, useCase: useCase)
print(String(format: "Use case: [%@]. Input: %@ -> Output: %@. Probability: %.2f %%",
useCase.truthTable.truth.joined(separator: ", "),
useCase.circuit.input,
useCase.circuit.output,
(probs[useCase.circuit.output] ?? 0.0) * 100))
}
Check full code in Genetic.playground.
Two-level decomposition: Decompose any gate into an equivalent sequence faster to execute
When it comes to get the statevector produced by a circuit, single-qubit gates & fully controlled matrix gates (i.e. controlled matrix gates where all inputs but one are controls) can be simulated faster. This algorithm decomposes any gate/s into an equivalent sequence of not gates and fully controlled gates. In most cases, the new sequence will be faster to execute than the original.
import SwiftQuantumComputing // for macOS
let factory = MainCircuitFactory(statevectorConfiguration: .elementByElement(maxConcurrency: 4))
let drawer = MainDrawerFactory().makeDrawer()
//: 1. Define gates
let gates = [
Gate.oracle(truthTable: ["0000", "1010"], controls: [7, 5, 2, 10], gate: .not(target: 0)),
Gate.oracle(truthTable: ["0011", "1100"], controls: [6, 10, 0, 1], gate: .not(target: 3)),
Gate.oracle(truthTable: ["1100", "1001"], controls: [3, 7, 4, 0], gate: .not(target: 10))
]
//: 2. (Optional) Draw gates to see how they look
drawer.drawCircuit(gates).get()
//: 3. Build circuit and measure how long it takes to get the statevector
var start = CFAbsoluteTimeGetCurrent()
factory.makeCircuit(gates: gates).statevector().get()
var diff = CFAbsoluteTimeGetCurrent() - start
print("Original circuit executed in \(diff) seconds")
//: 4. Decompose gates into an equivalent sequence of fully controlled matrix gates and not gates
start = CFAbsoluteTimeGetCurrent()
let decomposition = TwoLevelDecompositionSolver.decomposeGates(gates).get()
diff = CFAbsoluteTimeGetCurrent() - start
print("Original circuit decomposed in \(diff) seconds")
//: 5. (Optional) Draw decomposition to see how it looks
drawer.drawCircuit(decomposition).get()
//: 6. Build a new circuit and measure how long it takes to get the statevector. Statevector calculation is optimized
//: for the type of gates returned in the decomposition
start = CFAbsoluteTimeGetCurrent()
factory.makeCircuit(gates: decomposition).statevector().get()
diff = CFAbsoluteTimeGetCurrent() - start
print("Decomposed circuit executed in \(diff) seconds")
Check full code in TwoLevelDecomposition.playground.
Euclidean Algorithm: Find greatest common divisor of two integers
import SwiftQuantumComputing // for macOS
//: 1. Define two integers
let a = 252
let b = 105
//: 2. Use Euclidean solver to find greatest common divisor of these integers
let gcd = EuclideanSolver.findGreatestCommonDivisor(a, b)
print("Greatest common divisor of \(a) & \(b): \(gcd)")
Check full code in EuclideanAlgorithm.playground.
Continued Fractions: Find an approximation to a given rational number
import SwiftQuantumComputing // for macOS
//: 1. Define rational value to approximate
let value = Rational(numerator: 15, denominator: 11)
//: 2. And a limit or maximum difference between approximation and original value
let limit = Rational(numerator: 1, denominator: 33)
//: 3. Use Continued Fractions solver to find a solution
let approximation = ContinuedFractionsSolver.findApproximation(of: value,
differenceBelowOrEqual: limit).get()
print("Approximation for \(value) (limit: \(limit)): \(approximation)")
Check full code in ContinuedFractions.playground.
Gaussian Elimination: Solve a system of XOR equations
import SwiftQuantumComputing // for macOS
//: 1. Define system of XOR equations:
//: * `x6 ^ x4 ^ x2 ^ x1 = 0`
//: * ` x4 ^ x0 = 0`
//: * `x6 ^ x5 ^ x2 ^ x0 = 0`
//: * ` x4 ^ x3 ^ x1 ^ x0 = 0`
//: * ` x5 ^ x3 ^ x0 = 0`
//: * ` x4 ^ x3 ^ x1 = 0`
//: * ` x5 ^ x4 ^ x2 ^ x1 ^ x0 = 0`
let equations = [
"1010110",
"0010001",
"1100101",
"0011011",
"0101001",
"0011010",
"0110111"
]
//: 2. Build Gaussian elimination solver
let solver = MainXorGaussianEliminationSolverFactory().makeSolver()
//: 3. Use solver
print("Solutions: \(solver.findActivatedVariablesInEquations(equations))")
Check full code in XorGaussianElimination.playground.
Examples
Check following playgrounds for more examples:
- BernsteinVaziraniAlgorithm.playground - Bernstein–Vazirani algorithm.
- DeutschAlgorithm.playground - Deutsch's algorithm.
- DeutschJozsaAlgorithm.playground - Deutsch-Jozsa algorithm.
- GroverAlgorithm.playground - Grover's algorithm.
- ShorAlgorithm.playground - Shor's Algorithm.
- SimonPeriodicityAlgorithm.playground - Simon's periodicity algorithm.