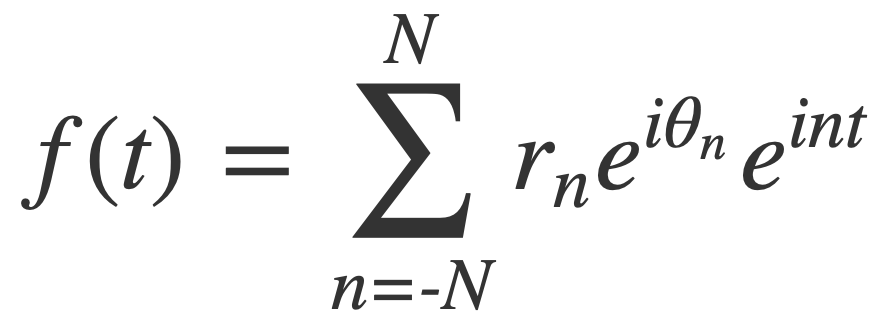Epicycles
Fourier coefficients of 2D curves are generated with numerical integration and displayed with epicycles.
The associated Xcode project implements an iOS and macOS SwiftUI app that numerically calculates the Fourier series of sampled parametric curves (x(t), y(t)) in the plane, points drawn by the user, or the samples of finite Fourier series created with a terms editor.
Experiment with complex Fourier series of the form:
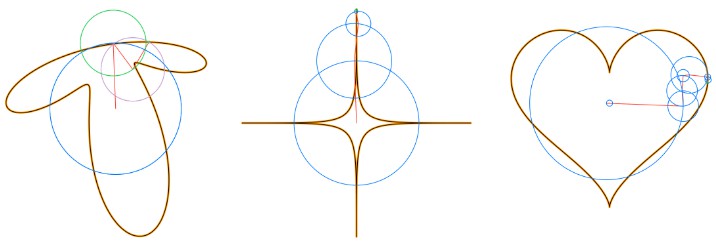
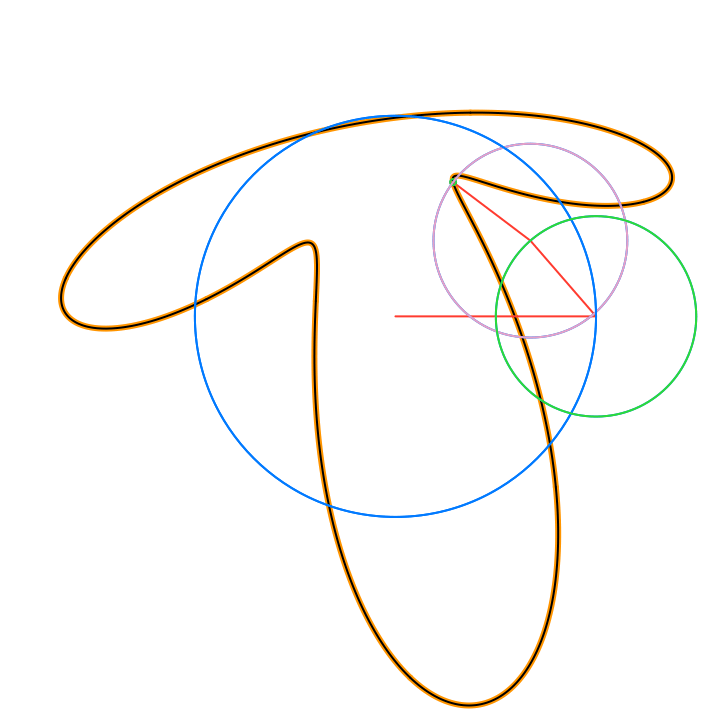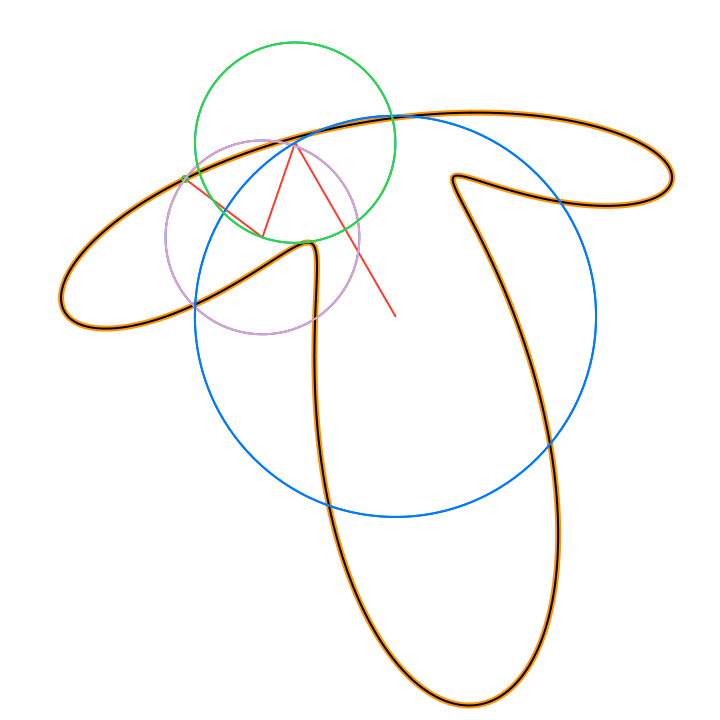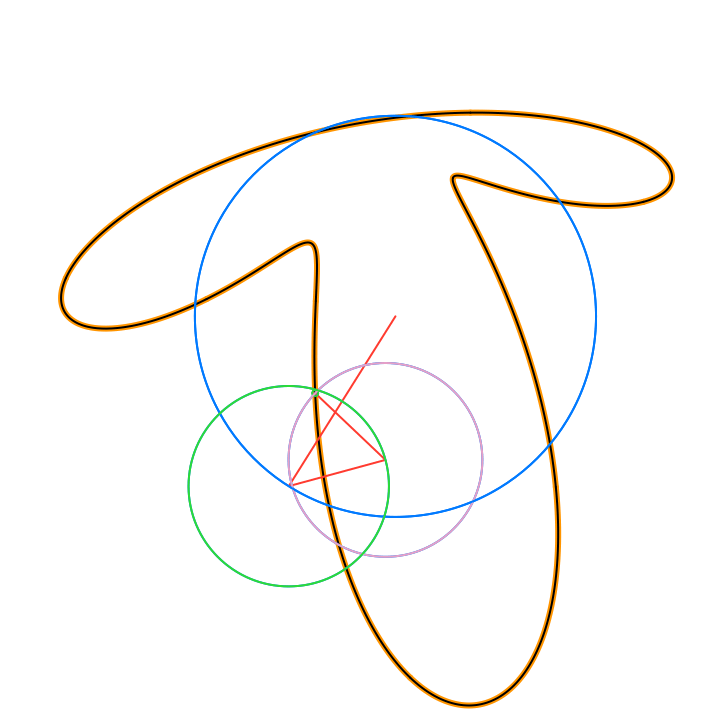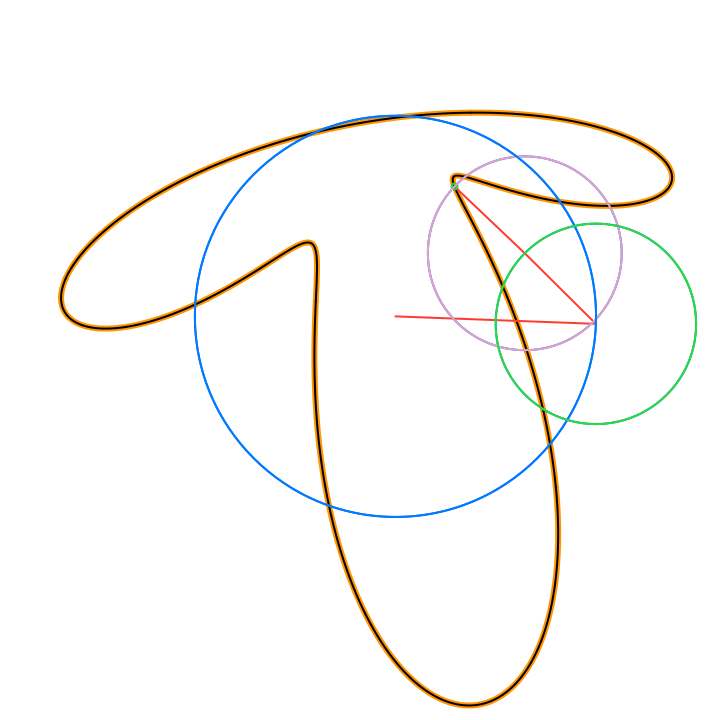
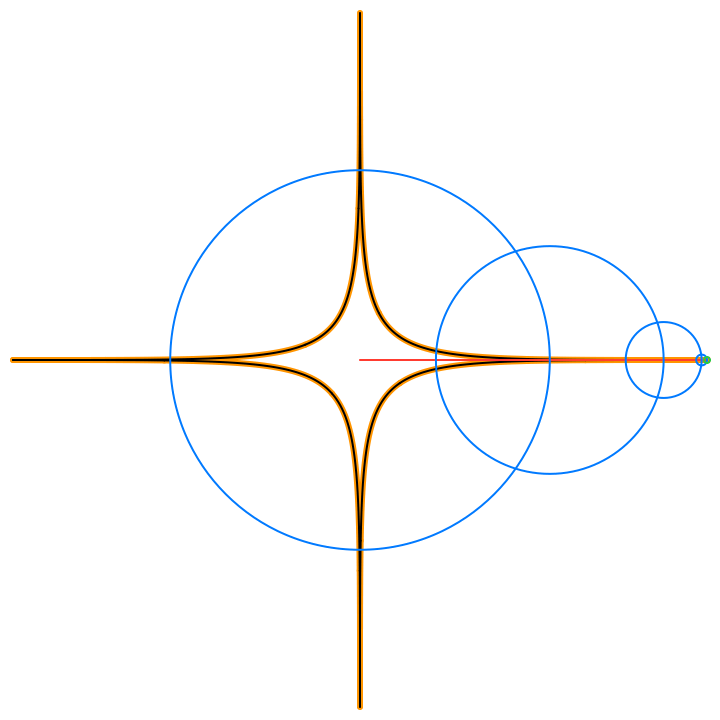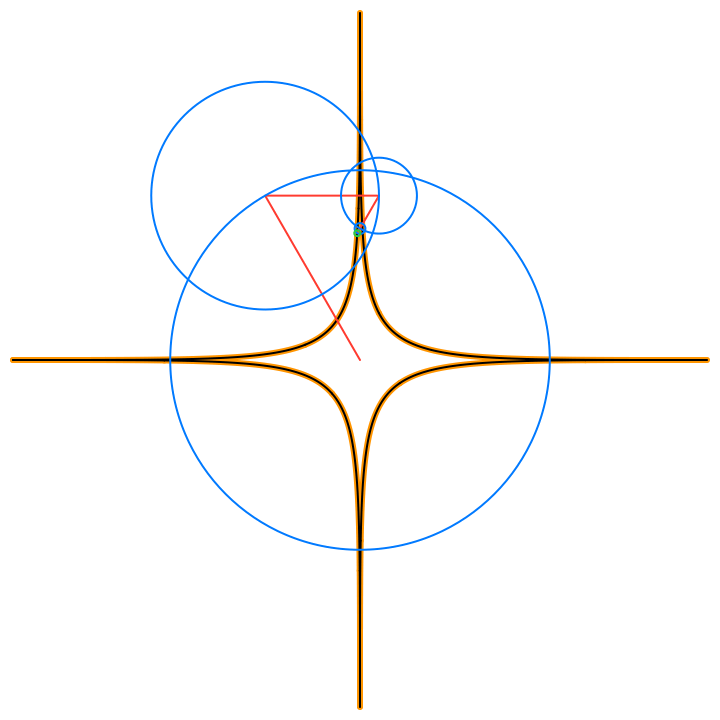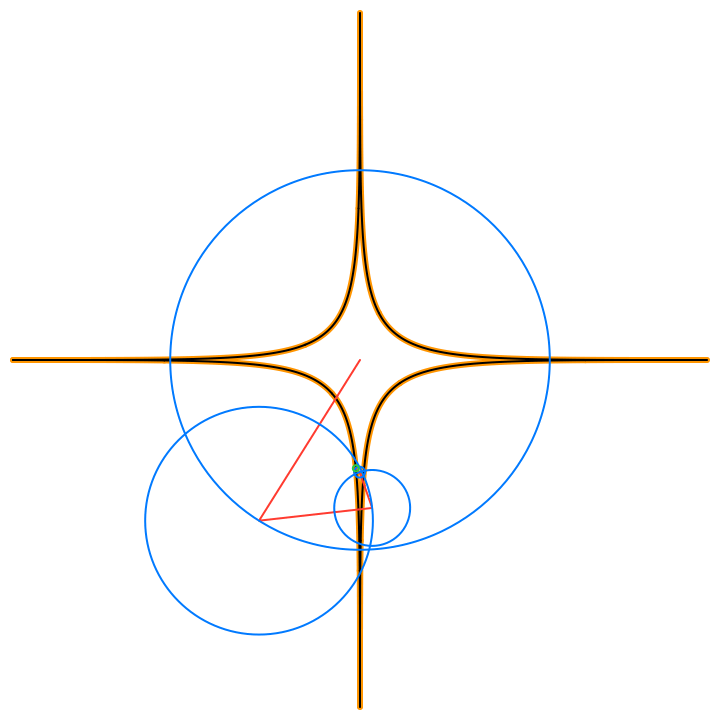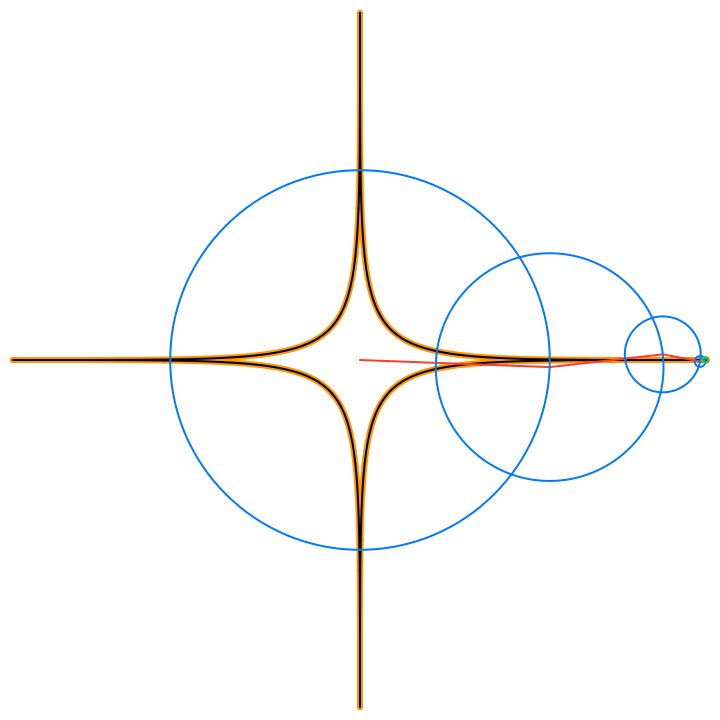
By Euler’s formula the n-th term (or frequency component) of the Fourier series is a complex number that traces a circle with radius rn in the 2D plane n times as t traverses an interval (period) of length 2π. The values of the sum trace the path of the function f(t) as t traverses an interval (period) of length 2π:
 |
 |
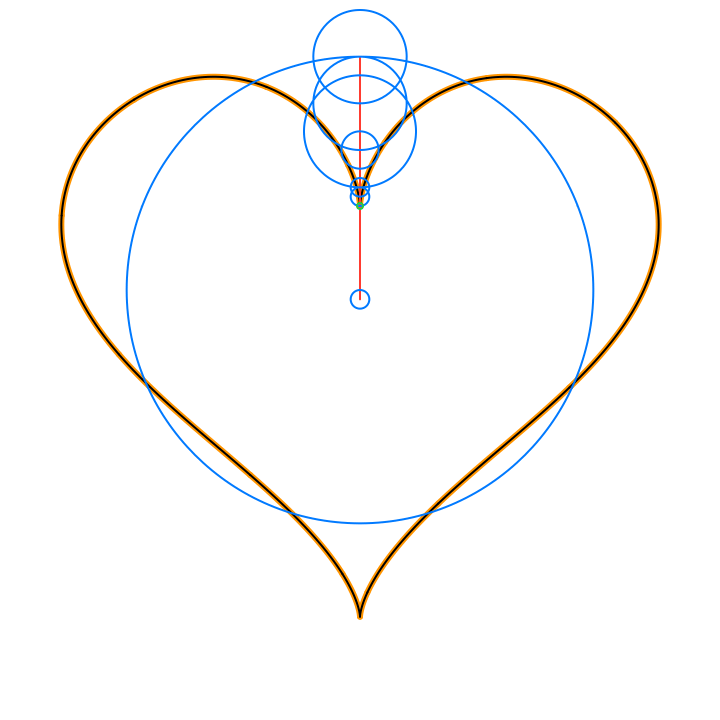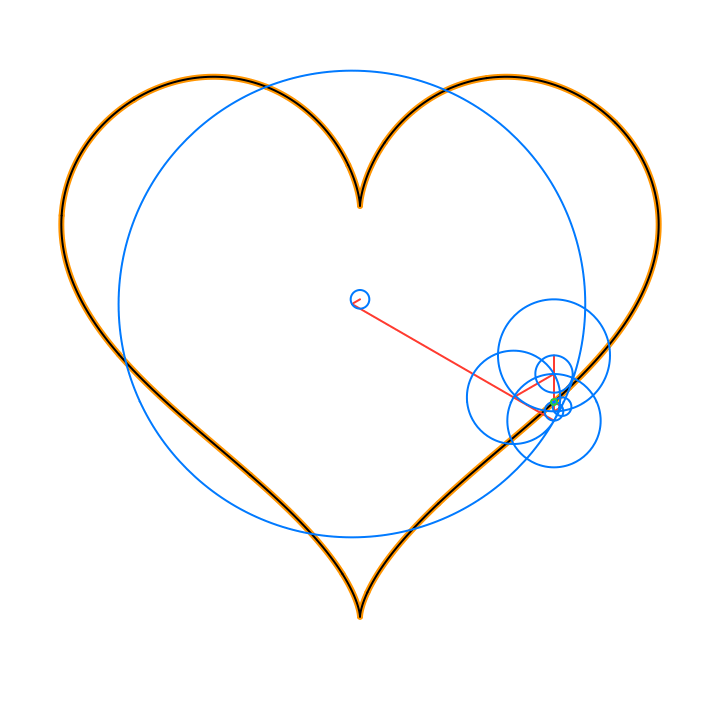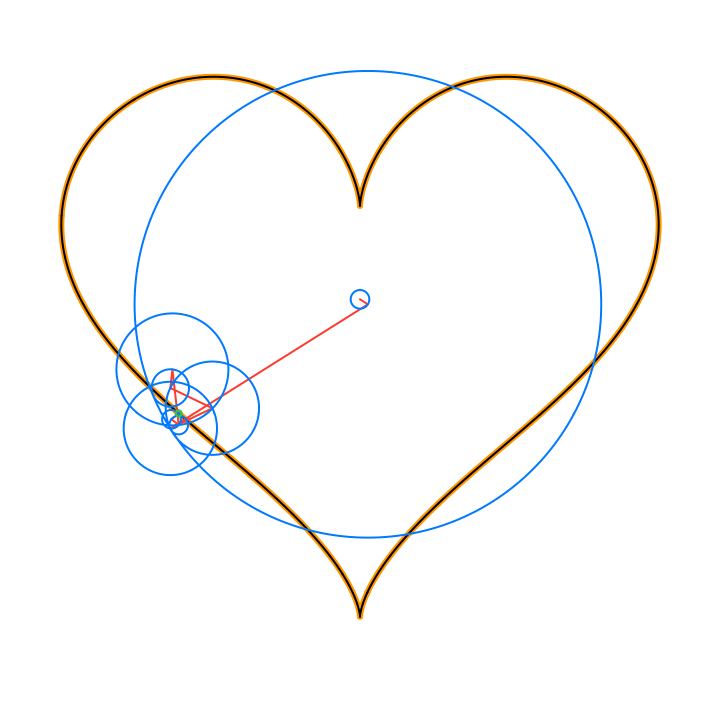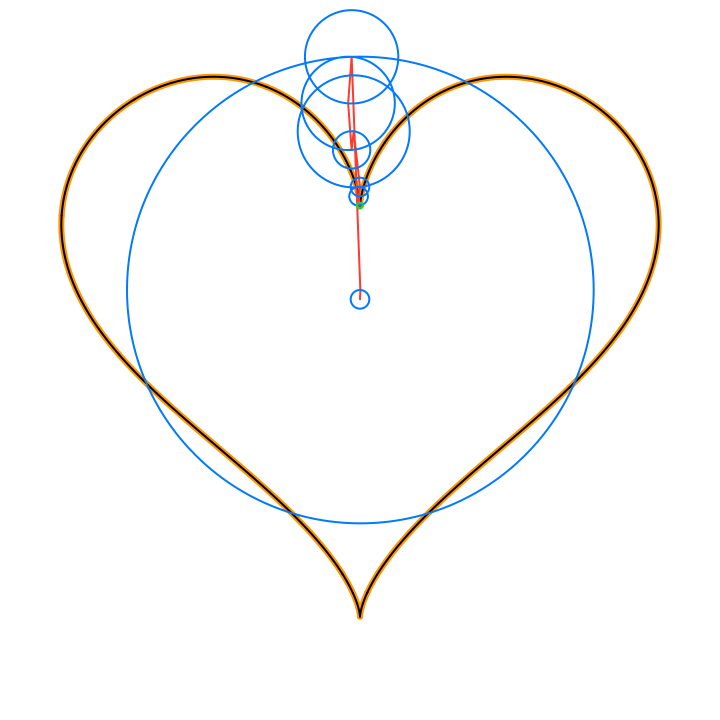 |
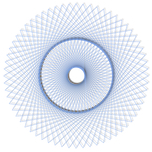
The circles in these animations that rotate on top of other circles are called epicycles. Each epicycle corresponds to a term of the complex Fourier series. The origin is at the constant term n = 0.